Inequality proving, crucial across diverse scientific and mathematical fields, tests advanced reasoning skills such as discovering tight bounds and strategic theorem application. This makes it a distinct, demanding frontier for large language models (LLMs), offering insights beyond general mathematical problem-solving. Progress in this area is hampered by existing datasets that are often scarce, synthetic, or rigidly formal. We address this by proposing an informal yet verifiable task formulation, recasting inequality proving into two automatically checkable subtasks: bound estimation and relation prediction.

Building on this, we release IneqMath, an expert-curated dataset of Olympiad-level inequalities, including a test set and training corpus enriched with step-wise solutions and theorem annotations. We also develop a novel LLM-as-judge evaluation framework, combining a final-answer judge with four step-wise judges designed to detect common reasoning flaws.

A systematic evaluation of 29 leading LLMs on IneqMath reveals a surprising reality: even top models like o1 achieve less than 10% overall accuracy under step-wise scrutiny; this is a drop of up to 65.5% from their accuracy considering only final answer equivalence. This discrepancy exposes fragile deductive chains and a critical gap for current LLMs between merely finding an answer and constructing a rigorous proof. Scaling model size and increasing test-time computation yield limited gains in overall proof correctness. Instead, our findings highlight promising research directions such as theorem-guided reasoning and self-refinement.

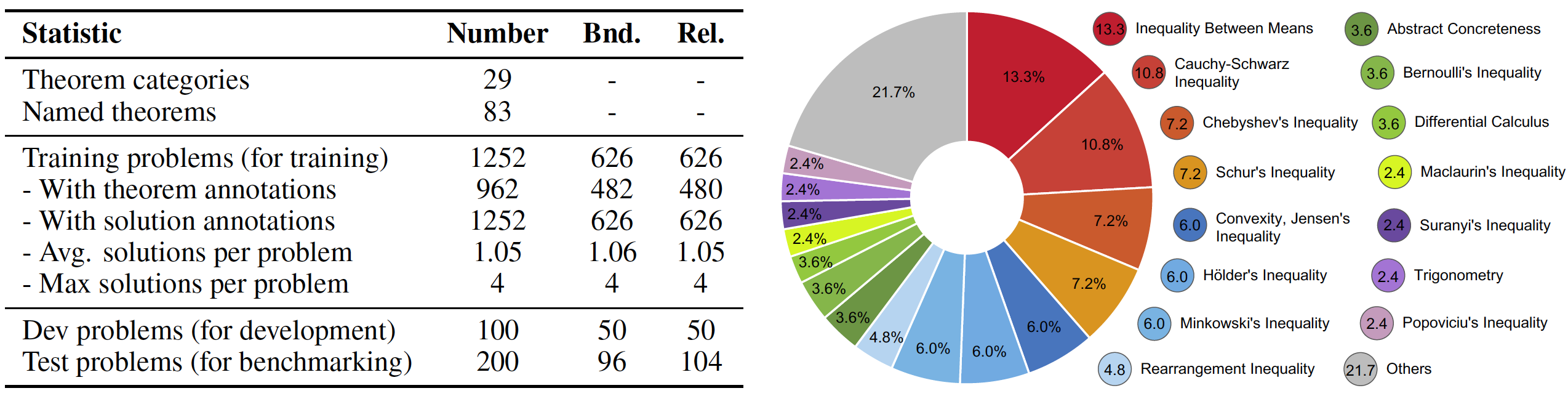
Below are training and testing examples from IneqMath. Each problem belongs to one of two automatically checkable subtasks: bound estimation or relation prediction. Each training problem includes step-wise solutions, with up to four solutions per problem, and 76.8% (962 problems) are annotated with relevant theorems. The test problems are each crafted and reviewed by IMO-level medalists to ensure both originality and difficulty.

Traditional evaluation methods fall short in this setting: expert annotation is accurate but prohibitively labor-intensive, while automated techniques such as string matching or value equivalence fail to capture step-by-step correctness—an essential aspect of inequality problem solving. To evaluate the correctness of IneqMath solutions, we propose a fine-grained LLM-as-judge framework, consisting of a final-answer judge for verifying the predicted answer and four specialized step-wise judges targeting common reasoning flaws. A solution is deemed correct overall only if it passes all five judges.

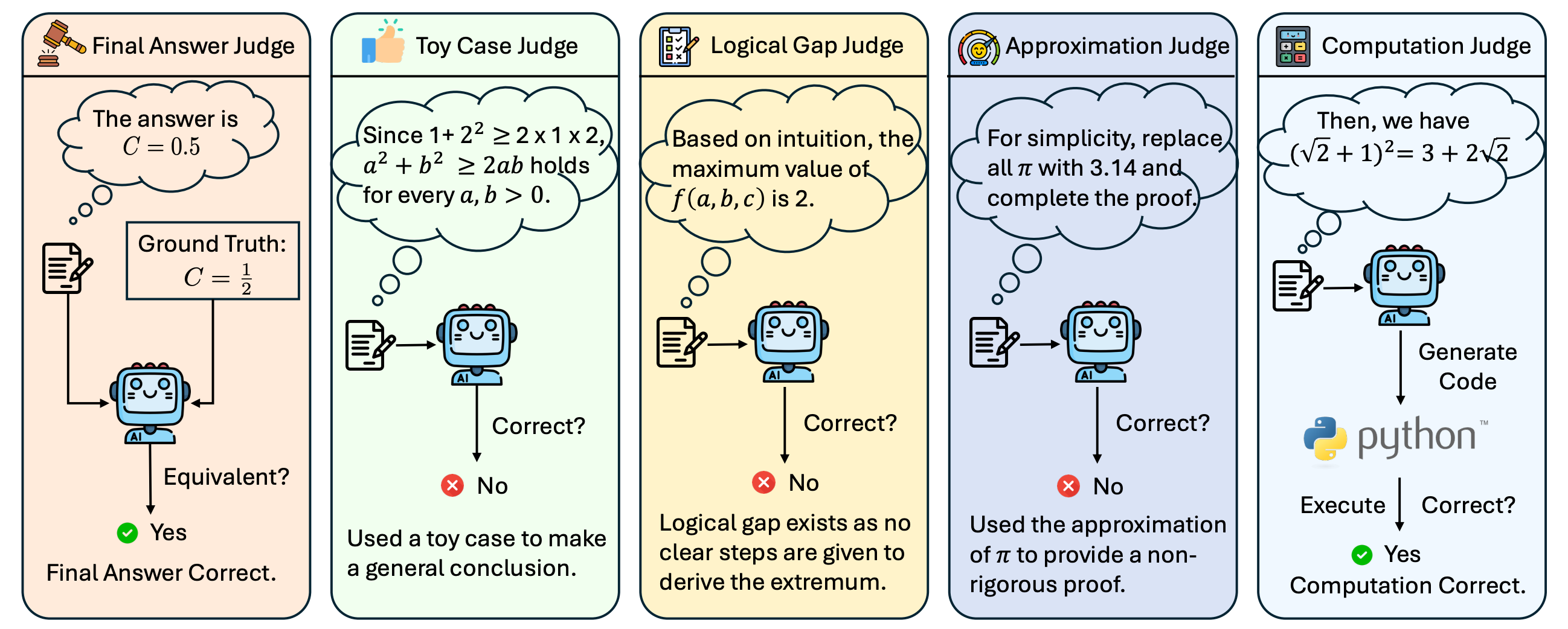
Illustration of the fine-grained LLM-as-judge framework. The framework combines a Final Answer Judge with four step-wise judges: Toy Case Judge, Logical Gap Judge, Numerical Approximation Judge (shown as Approximation Judge), and Numerical Computation Judge (shown as Computation Judge). A solution is considered correct only if it passes all five judges.

We also conducted a systematic evaluation of these judges on the development set. As shown in the following table and confusion matrix, these judges achieve strong alignment with human annotations (F1 = 0.93), providing a scalable yet reliable alternative to manual evaluation.

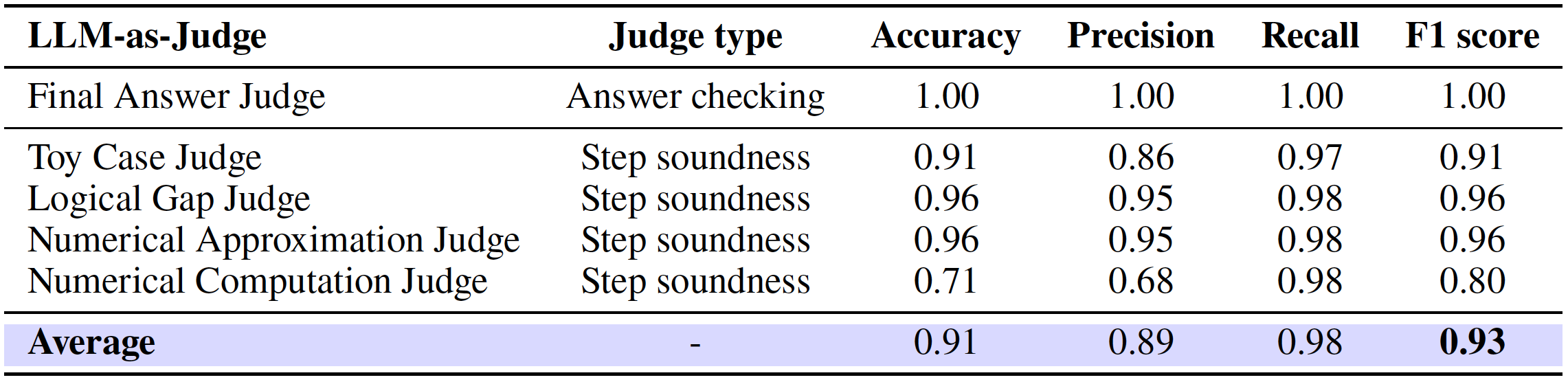
Performance metrics of LLM-as-Judge framework on development set.

Confusion matrices for five judges on development set, which exhibit strong agreement with human labels.

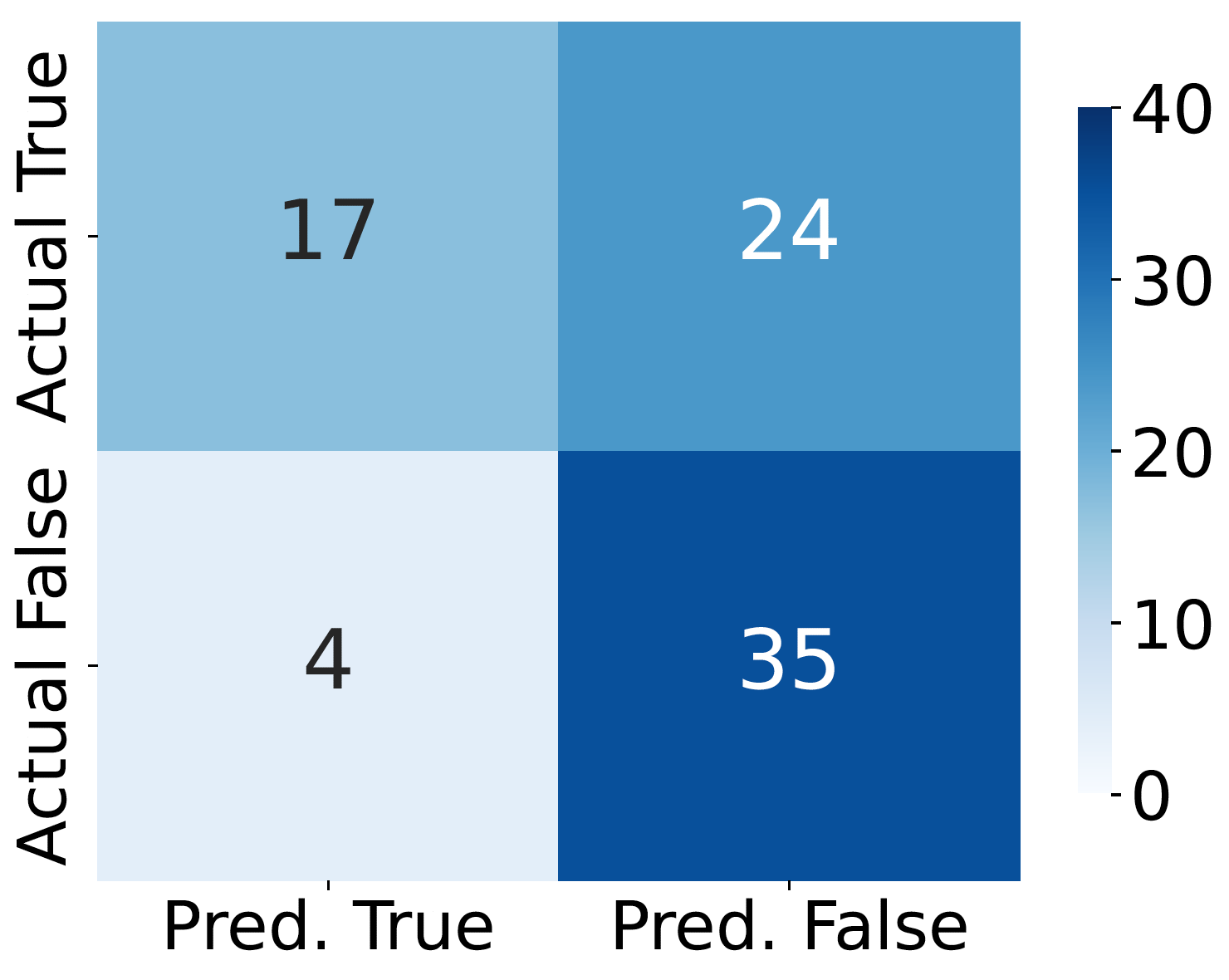
Confusion matrix for the judge baseline. The baseline is a single, general-purpose LLM to holistically assess IneqMath solution correctness, based on both final answer accuracy and step-wise soundness.

The IneqMath dataset comprises 200 test problems for benchmarking, 100 development problems with public ground truth, and 1,252 training problems split evenly between bound estimation and relation prediction tasks, as shown in the table below. The dataset also features 83 named theorems across 29 categories, with their distribution illustrated in the figure below.

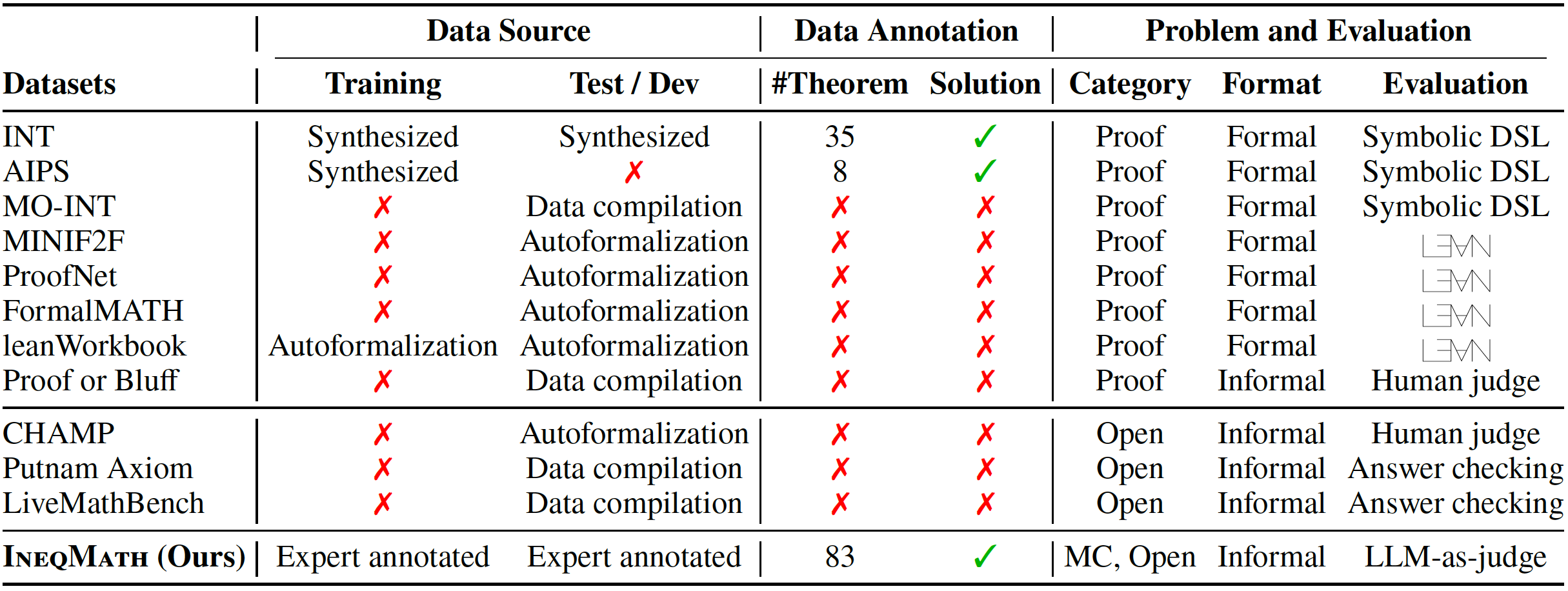
The table below is a comparison of datasets for inequalities and theorem proving. IneqMath provides expert-annotated training and test/dev sets, featuring high-quality named theorems and step-wise solutions for model development. Unlike prior datasets using synthesis or autoformalization, IneqMath presents problems in informal language across multiple-choice (MC) and open-ended (Open) formats, and employs LLM-as-judge for evaluation.

We conduct a systematic evaluation of 29 leading LLMs on the inequality problems in the IneqMath test set. The evaluated models span two categories: general-purpose chat models (both open-source and proprietary) and specialized reasoning LLMs designed for complex, multi-step problem-solving. All models are prompted in a zero-shot setting with the problem statement and the instruction: "Please solve the problem with clear, rigorous, and logically sound steps" to encourage detailed reasoning. The table below presents the performance of the evaluated LLMs on IneqMath. Our analysis reveals several critical insights into current LLM capabilities for inequality proving:

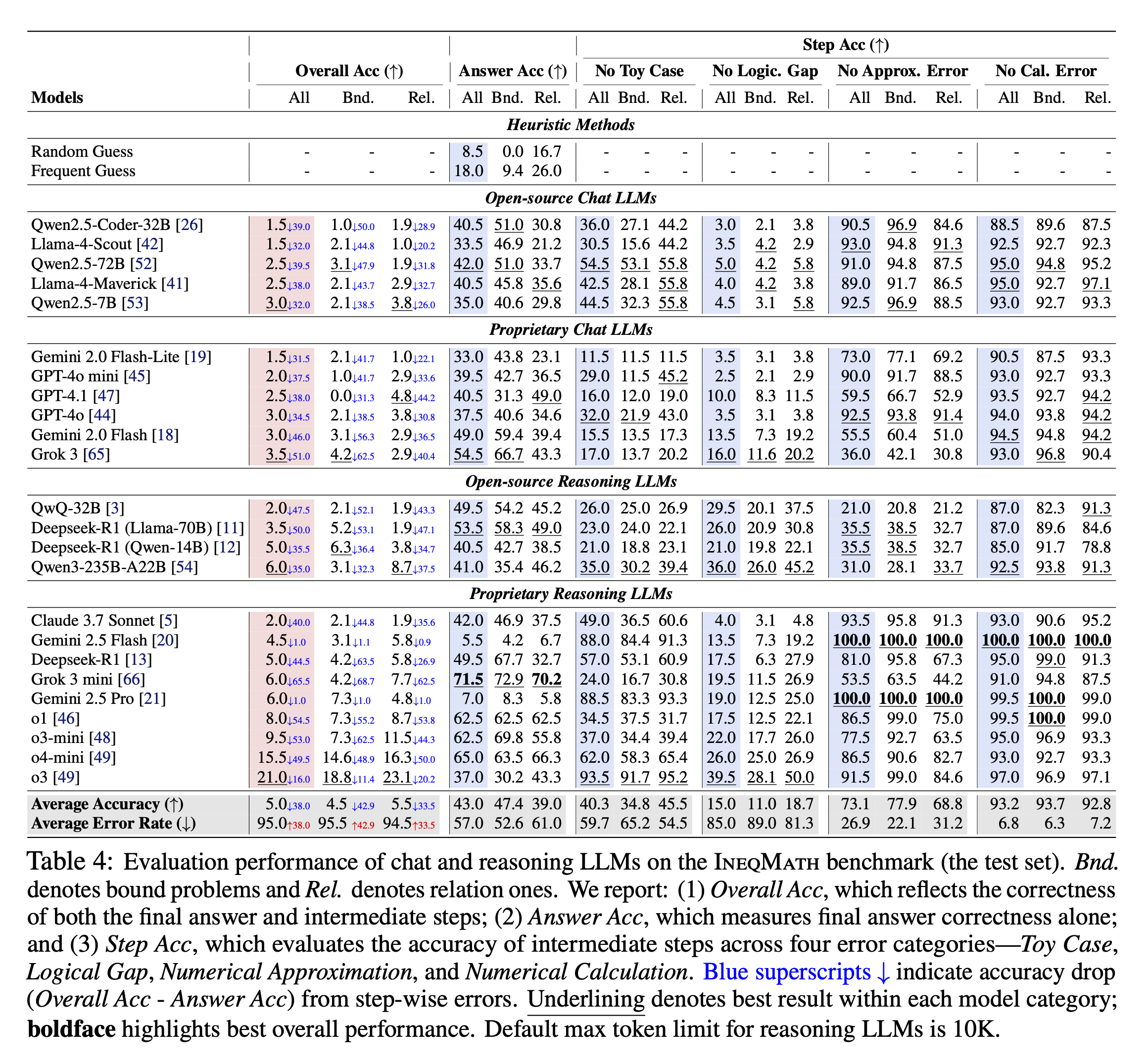
Evaluation performance of chat and reasoning LLMs on the IneqMath benchmark (the test set). Bnd. denotes bound problems and Rel. denotes relation ones. We report: (1) Overall Acc, which reflects the correctness of both the final answer and intermediate steps; (2) Answer Acc, which measures final answer correctness alone; and (3) Step Acc, which evaluates the accuracy of intermediate steps across four error categories—Toy Case, Logical Gap, Numerical Approximation, and Numerical Computation. Blue superscripts ↓ indicate accuracy drop (Overall Acc - Answer Acc) from step-wise errors. Underlining denotes best result within each model category; boldface highlights best overall performance. Default max token limit for reasoning LLMs is 10K.

We conduct an in-depth analysis to understand the performance characteristics and limitations of current models on IneqMath. Our study encompasses three key areas: scaling laws in model size to examine how model size affects reasoning accuracy, scaling laws in test-time computation to investigate the impact of extended reasoning chains, and few-shot evaluation to assess how the use of example demonstrations affects model performance. These analyses reveal critical insights into the challenges of inequality proving and provide guidance for improving mathematical reasoning capabilities.

Scaling laws in model size: This figure shows how final-answer accuracy (which evaluates only the correctness of the final predicted answer) scales with model size for LLMs. As model size increases, we observe a steady improvement in answer accuracy, reflecting an empirical scaling law: larger models are better at inferring correct final answers.

Scaling laws in model size: However, the trend for answer accuracy does not hold for overall accuracy—which requires both a correct answer and valid intermediate reasoning steps—as shown in the figure above. In this case, the scaling curve flattens, indicating that increased model size alone is insufficient to eliminate step-by-step reasoning errors.

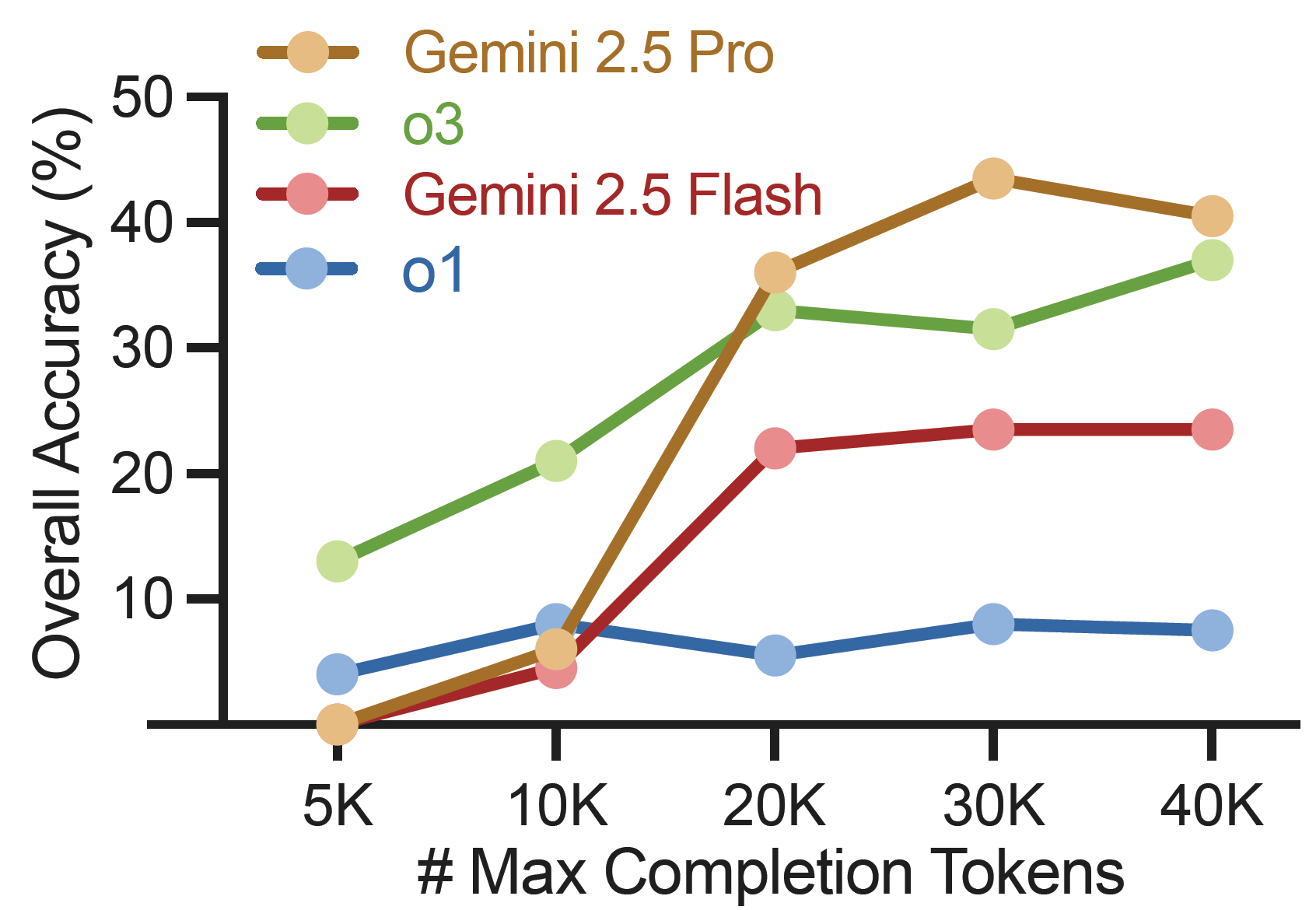
Scaling laws in test-time computation: The figure above shows that while models like Gemini 2.5 Pro and o3 initially improve with more tokens, performance gains saturate (e.g., beyond 20K tokens). This indicates that merely increasing computational budget offers diminishing returns for achieving rigorous, step-wise correct proofs, highlighting the need for more than just longer thought processes.

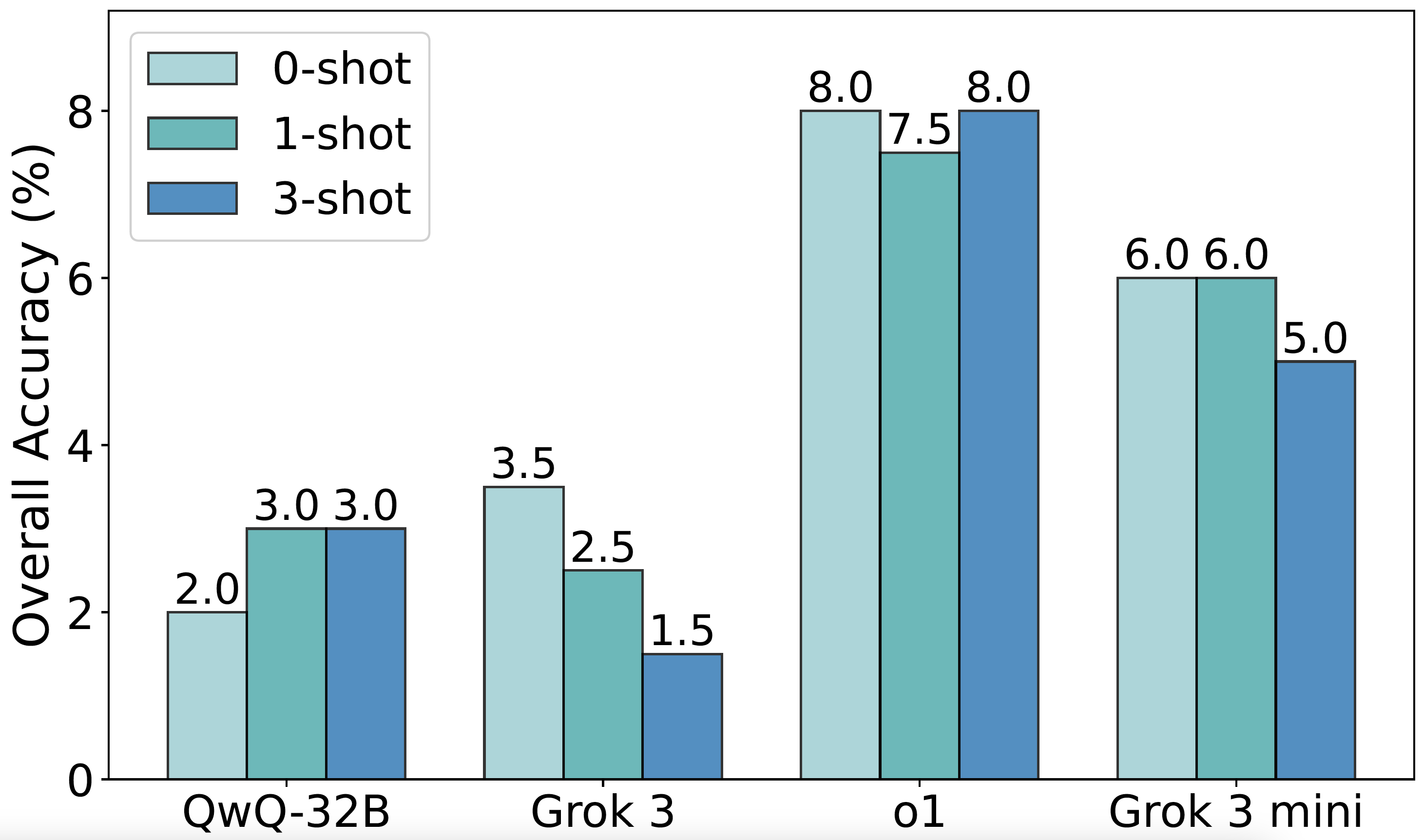
Few-shot evaluation: The gains in overall accuracy from few-shot prompting were small, typically below 2% compared to zero-shot performance. For instance, Grok 3 achieved 3.5% accuracy in the zero-shot setting but dropped slightly in the one-shot and three-shot settings (2.5% and 1.5%, respectively). Similarly, o1 peaked at 8.0% in both the one-shot and three-shot settings, with minimal difference across shots.

Few-shot evaluation: Moreover, the few-shot prompting typically reduces answer accuracy. For o1, accuracy drops from 62.5% in the zero-shot setting to 55.5% with one-shot and 53.0% with three-shot. QwQ-32B displays the same trend: both one-shot and three-shot underperform the zero-shot baseline (41.5% and 43.5% vs. 49.5%).

We explore four promising strategies to enhance LLM performance on IneqMath: retrieving relevant theorems as hints, self-improvement via critic as feedback, taking annotated theorems as hints, and retrieving training problems as demonstrations.

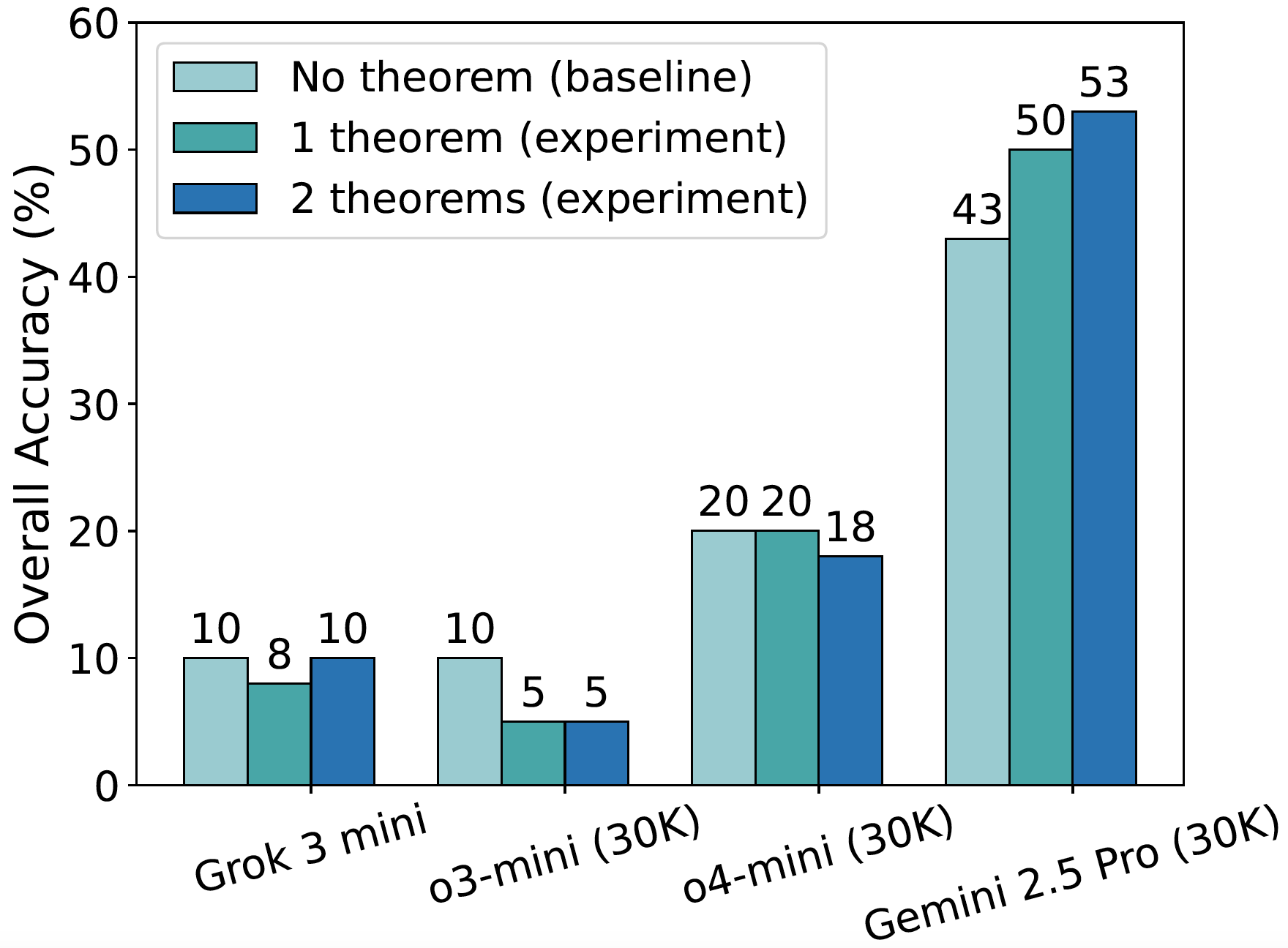
Retrieving relevant theorems as hints: As shown in the figure, providing one or two such theorems decreases overall accuracy for weaker models (e.g., Grok 3 mini, o3-mini, o4-mini), likely due to misapplication or distraction by potentially irrelevant information. Conversely, stronger models like Gemini 2.5 Pro benefit from these hints, suggesting advanced reasoning is crucial to effectively use such guidance. These results underscore the potential of theorem-guided reasoning but also highlight the critical need for more sophisticated theorem retrieval mechanisms (e.g., RAG) to reliably enhance LLM performance in inequality proving.

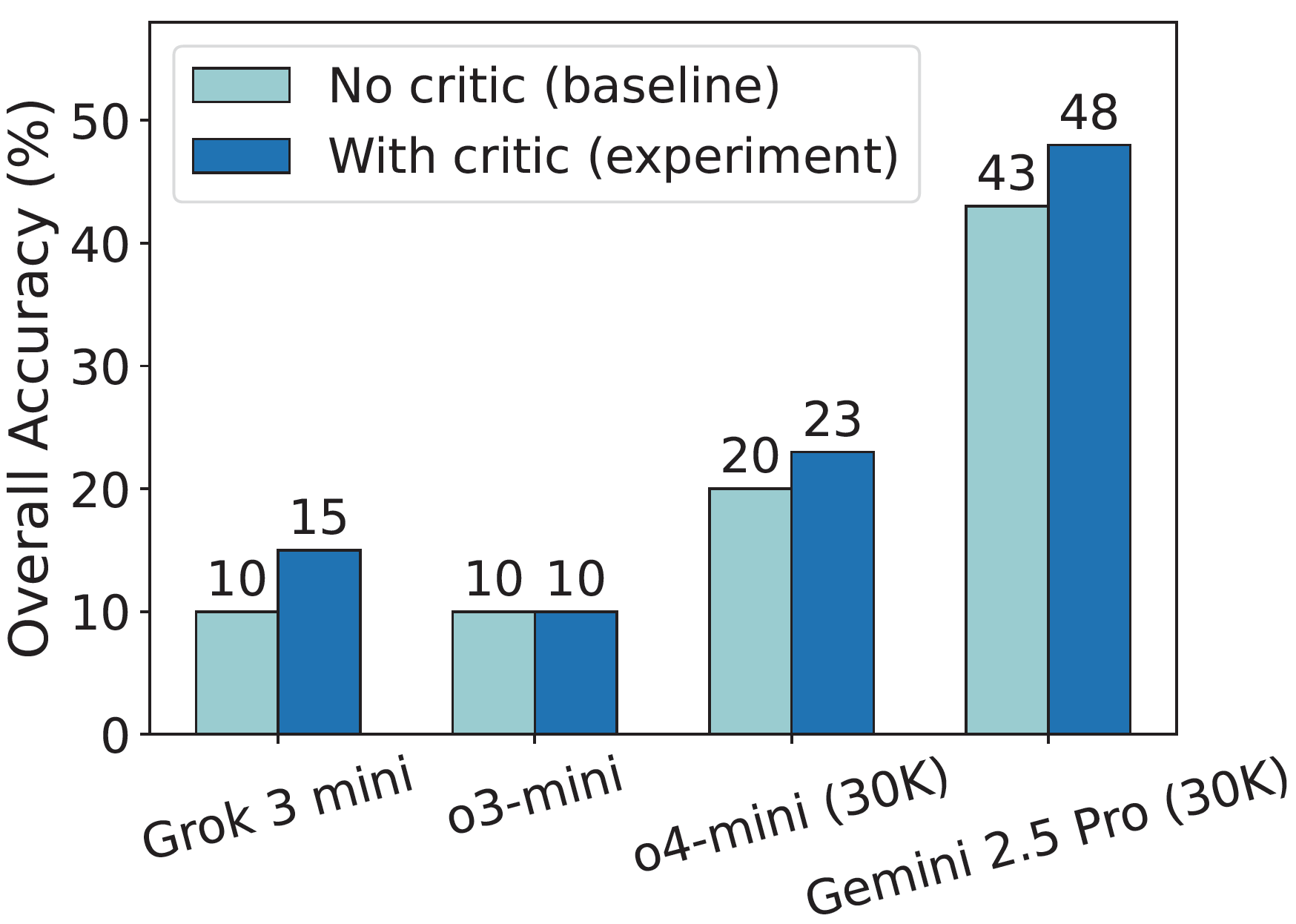
Self-improvement via critic as feedback: As the figure shows, self-critique consistently improves performance—e.g., Gemini 2.5 Pro's overall accuracy rises from 43% to 48%. This upward trend underscores self-critique as a promising, supervision-free method to enhance the logical rigor and solution quality of LLMs in inequality reasoning.

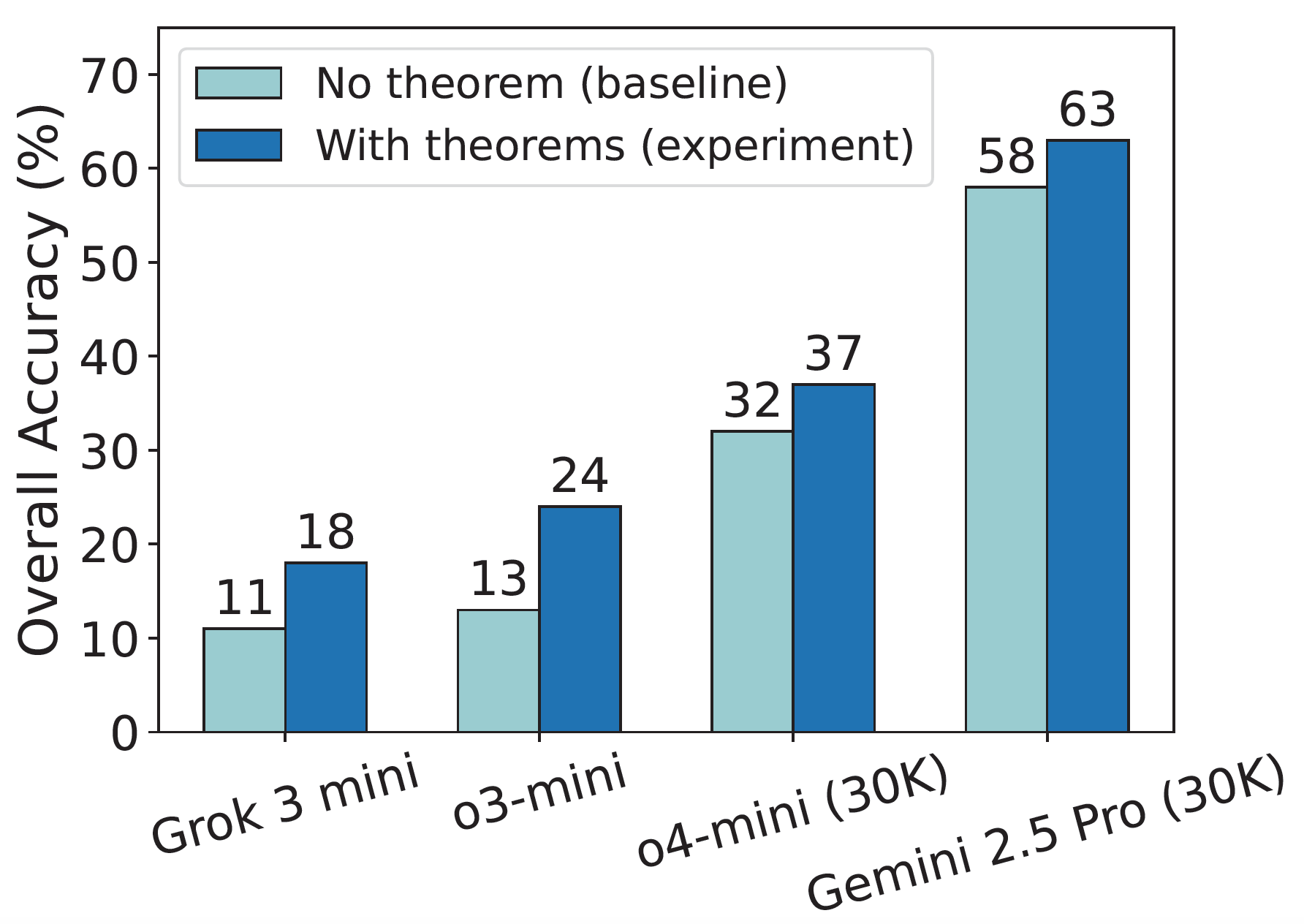
Taking annotated theorems as hints: The figure reveals a consistent uplift in overall accuracy across models, with gains reaching up to 11% (e.g., for o3-mini).

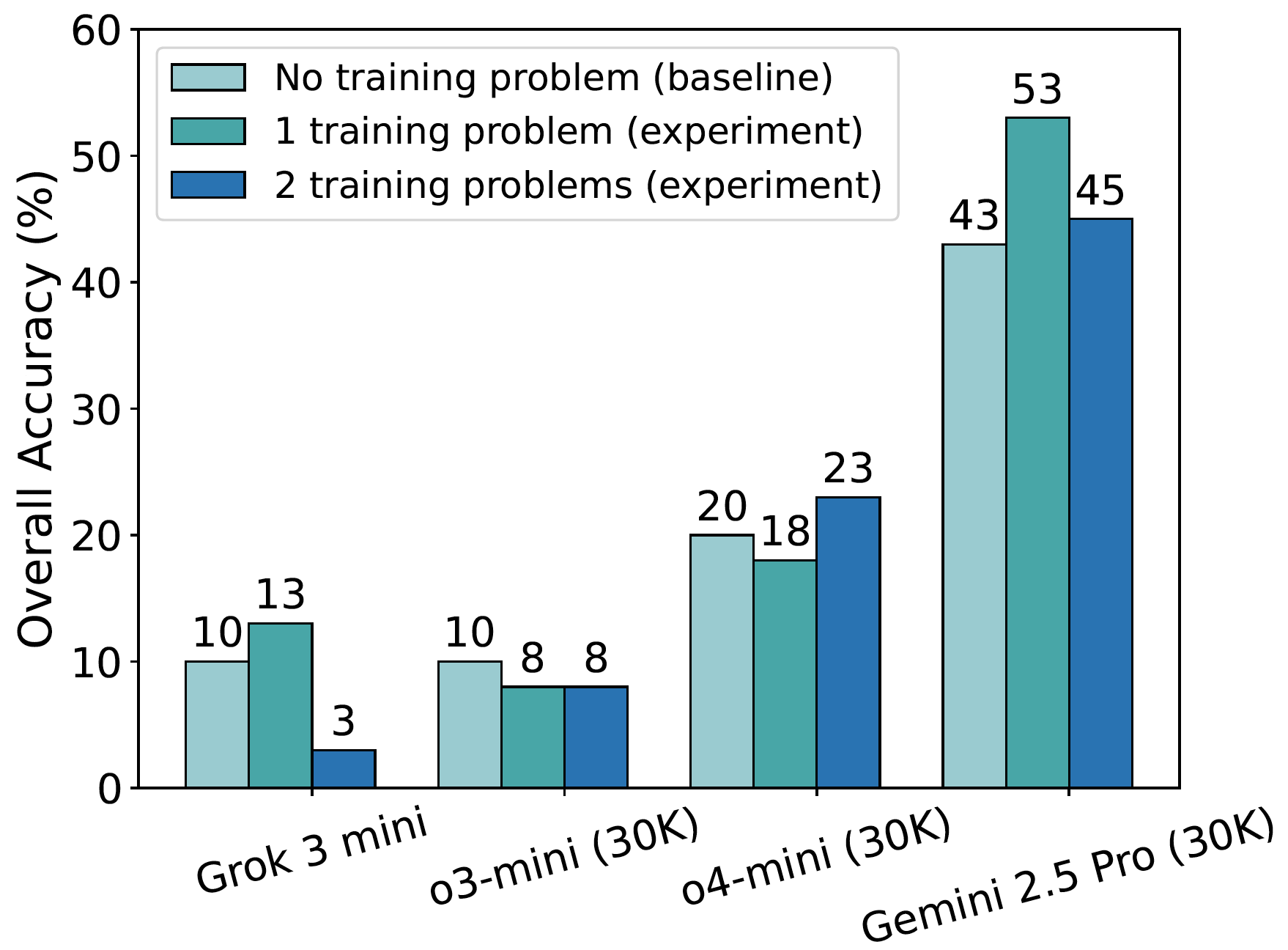
Retrieving training problems as demonstrations: As shown by the overall accuracy in the figure, Grok 3 mini's performance improves from a baseline of 10% (with no demonstration problem) to 13% when provided with one such problem. However, its accuracy drops sharply to 3% when two problems are used as demonstrations. Similarly, Gemini 2.5 Pro peaks at 53% accuracy with one demonstration problem, declining to 45% with two. o4-mini reaches 23% accuracy with one demonstration problem, a 3% increase from its 20% baseline (without demonstrations).

To expand the impact of IneqMath, we conduct a formal evaluation on state-of-the-art automated theorem proving (ATP) models. We convert the natural language inequality problems in IneqMath into machine-verifiable Lean4 code as illustrated below. Then, we evaluate the SOTA models on the formalized Lean4 problems to measure their ability to solve inequality tasks with pass@32 setting.

The results below show that state-of-the-art (SOTA) formal automated theorem proving models still suffer from the difficult inequality problems in IneqMath. Even the best-performing model, Goedel-Prover-SFT, achieves only a 14.0% pass rate, while others remain far lower.

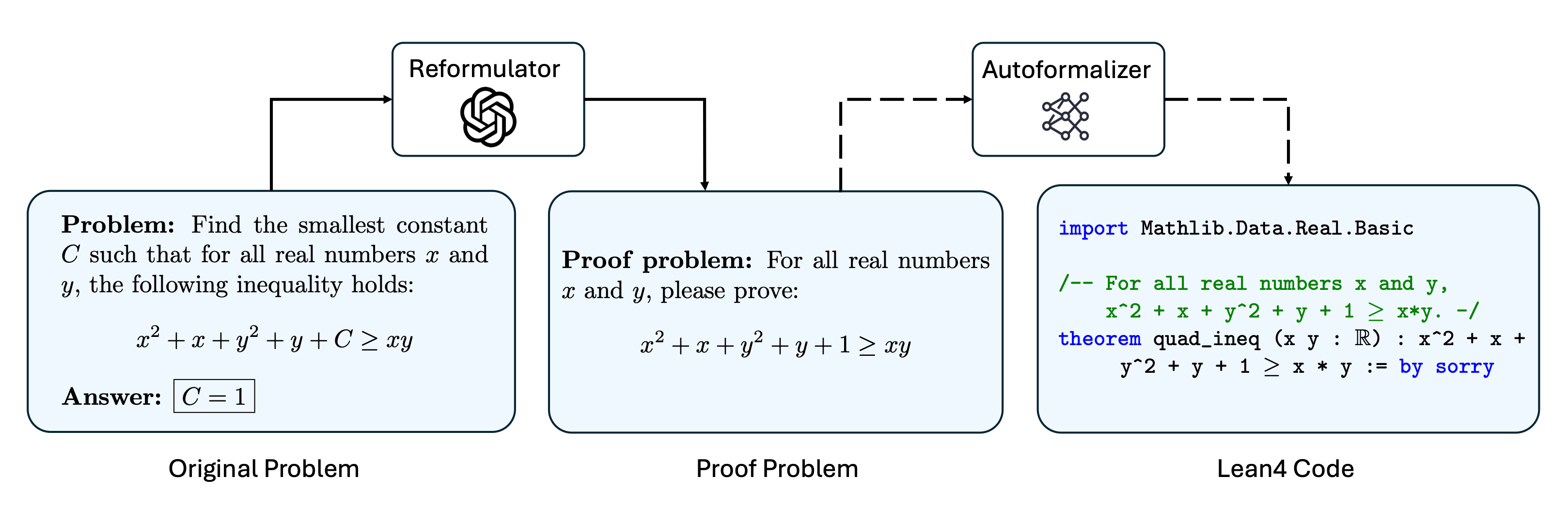
Illustration of the formalization process for bound problems.

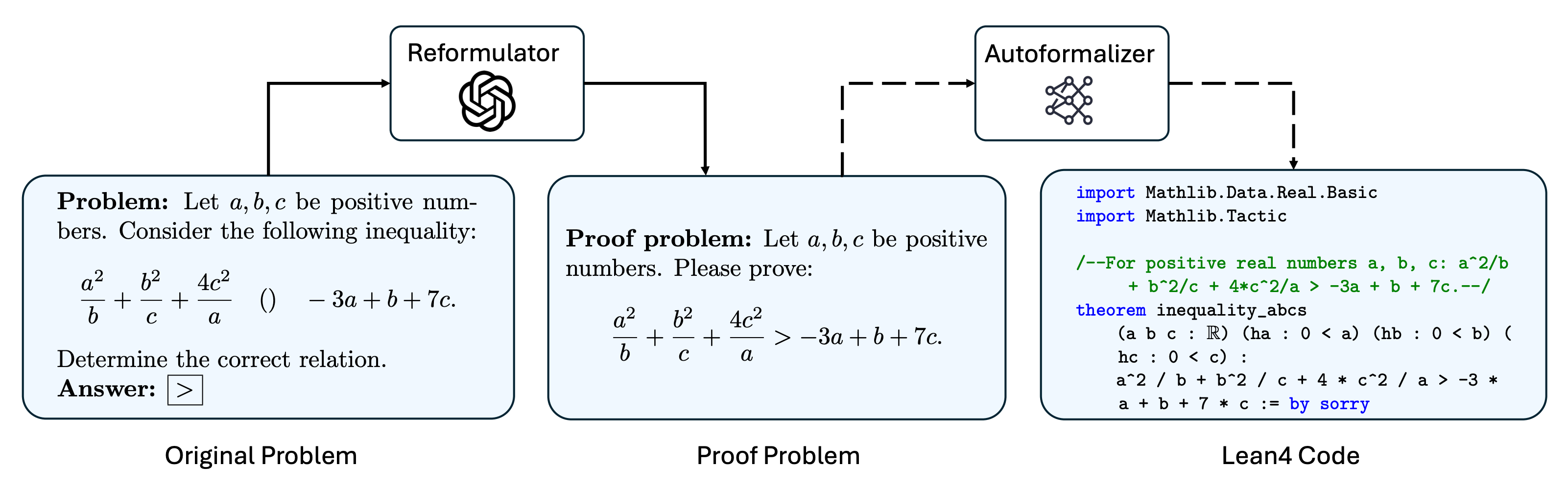
Illustration of the formalization process for relation problems.

Pass@32 performance of state-of-the-art formal automated theorem proving models.